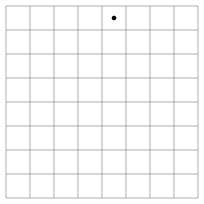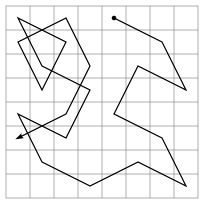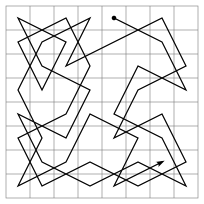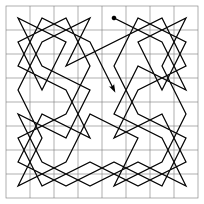
The Knight's Tour

(November 2008)

When I was a kid, I used to play chess with my older brothers. Since they were much older than me, I was more or less a "punch bag", and was losing the matches in (usually) a matter of minutes. I was persistent though... and saddened by defeat after defeat, I occasionally "escaped" into the solitary game of the Knight's Tour. From my local copy of Wikipedia:

The Knight's Tour is a mathematical problem involving a knight on a chessboard. The knight is placed on the empty board and, moving according to the rules of chess, must visit each square exactly once.

It was easy to understand, easy to try, but not so easy to accomplish. And it only required a pen and a piece of paper. Whenever I managed to complete all 64 squares (by shear luck), I always felt a surge of exhilaration.

Nowadays, I've more or less abandoned chess... But strangely enough, I remembered my childhood refuge once again today, just by seeing some Sudoku puzzle in a magazine... and decided to take another swing at it. With much better tools than pen and paper :‑)

Python attacks Knight

I started with this code:

#!/usr/bin/env python
import sys

g_sqSize = -1   # the board size, passed at runtime
g_board = []    # the board will be constructed as a list of lists

def main():
    global g_sqSize
    if len(sys.argv) != 2:
        g_sqSize = 8  # Default: Fill the normal 8x8 chess board
    else:
        try: g_sqSize = int(sys.argv[1]) # or, the NxN the user wants
        except:
            print("Usage: " + sys.argv[0] + " <squareSize>")
            sys.exit(1)
    for i in range(0, g_sqSize):
        g_board.append(g_sqSize*[0])  # Fill the board with zeroes
    Fill(0,0,1)    # Start the recursion with a 1 in the upper left
    print("No solution found")  # if the recursion returns, it failed

def InRangeAndEmpty(ty,tx):  # check if coordinates are within the board
    return ty>=0 and tx>=0 and ty<g_sqSize and tx<g_sqSize \
        and g_board[ty][tx] == 0 # and the square is empty

def Fill(y,x,counter): # The recursive function that fills the board
    assert g_board[y][x] == 0
    g_board[y][x] = counter          # Fill the square
    if counter == g_sqSize*g_sqSize: # Was this the last empty square?
        PrintBoard()                 # Yes, print the board...
        sys.exit(1)                  # ...and exit
    jumps = ((-2,1),(-1,2),(1,2),(2,1),(2,-1),(1,-2),(-1,-2),(-2,-1))
    for jump in jumps:  # otherwise, try all the empty neighbours in turn
        ty,tx = y+jump[0], x+jump[1]
        if InRangeAndEmpty(ty,tx):
            Fill(ty,tx,counter+1)    # *** RECURSION! ***
    g_board[y][x] = 0 # if we get here, all the neighbours failed,
                      # so reset the square and return

def PrintBoard(): # print the board using nice ASCII art ('+' and '-')
    scale = len(str(g_sqSize*g_sqSize))
    print(g_sqSize*("+" + scale*"-") + "+")
    for line in g_board:
        for elem in line:
            sys.stdout.write("|%*d" % (scale,elem))
        print("|\n"+g_sqSize*("+" + scale*"-") + "+")

if __name__ == "__main__":
    main()

The code performs a recursive attempt to Fill the board. Starting at the top left corner, it proceeds to identify the empty neighbours, trying each one of them in turn.

This naive approach is functional, but...

bash$ ./knight1.py 5
+--+--+--+--+--+
| 1|20|17|12| 3|
+--+--+--+--+--+
|16|11| 2| 7|18|
+--+--+--+--+--+
|21|24|19| 4|13|
+--+--+--+--+--+
|10|15| 6|23| 8|
+--+--+--+--+--+
|25|22| 9|14| 5|
+--+--+--+--+--+

...only for small boards. It solves the 5x5 and 6x6 boards in less than a second, but it takes 96 seconds to solve the 7x7 and 28 seconds to solve the 8x8... I didn't even try with larger board sizes, since it was clear that naive recursion is too slow.

I then proceeded to add some extra intelligence in the recursion, by filling the "lonesome" squares first:

...
emptyNeighbours = []  # find our empty neighbours for the recursion
jumps = ((-2,1),(-1,2),(1,2),(2,1),(2,-1),(1,-2),(-1,-2),(-2,-1))
for jump in jumps:
    ty,tx = y + jump[0], x + jump[1]
    if InRangeAndEmpty(ty,tx):
        emptyNeighbours.append([ty,tx])

# recurse using our neighbours, trying first the ones with the 
# least amount of free neighbours, i.e. the "loners"
for ty,tx in sorted(emptyNeighbours, key=lambda c: reduce(
    lambda x,y: x+y, 
    map(lambda j: InRangeAndEmpty(c[0]+j[0], c[1]+j[1]) and 1 or 0, 
        jumps))):
    Fill(ty,tx,counter+1)
...

I know, this code has 3 lambdas in 3 successive lines, I've gone a little too far :‑) Well, bear with me, what it does is in fact very simple. It sorts the emptyNeighbours list according to how "lonely" this neighbour is, that is, according to how many empty neighbours he has. To do that, it uses map to apply a lambda to all the elements of jumps: the innermost lambda checks in turn all neighbours to see if (a) they are within the board and (b) they are empty. If a neighbour fulfils both, the lambda returns 1, otherwise it returns 0. reduce is then used to accumulate all 1s (up to a maximum of 8) and return their sum (via the lambda x,y: return x+y). Finally, we use this calculation process as the sort key for the call to sorted(emptyNeighbours). In that way, the neighbouring empty squares that have the least "free space" around them, are used first during the recursion.

Python also offers the sum function to implement the accumulation process, and it also offers list comprehensions to ease up the syntax further:

for ty,tx in sorted(emptyNeighbours, key=lambda c: 
    sum([InRangeAndEmpty(c[0]+j[0], c[1]+j[1]) and 1 or 0 for j in jumps])):
    Fill(ty,tx,counter+1)
...

By using this simple policy (which I clearly remember I was also following when I was a kid!), the solving time became less than 100 milliseconds, for all square sizes up to 31x31! Beyond 31x31, at least on my manually-compiled Python interpreter, the program run out of stack space and required an increase in Python's recursion limit (via sys.setrecursionlimit). After that little tweak, the 100x100 problem was solved just as quick :‑)

P.S. Not to be paternalistic, but allow me to suggest writing this sorting code in C (using qsort?), or in C++ using STL's sort algorithm. When you finish, look at the code you wrote, and then look back at the Python code in its final form: 2 lines to implement the sorting! You'll have to agree that writing functions just to pass to qsort (or functors in order to pass to std::sort) is... well, far behind. Python syntax has tremendous advantages... Advantages that have nothing to do with libraries, and can be traced back to the combination of (a) functional programming concepts and (b) the perfect syntax that Python offers. I would truly be amazed to see anyone writing the same sorting logic in C++ in anything less than 3 times the lines of code I wrote for it in Python. And even if this is somehow possible (using external libraries like BOOST, I'd wager), the sorting code will take longer to write, and it will be far more difficult to comprehend or refactor...

It took me less than an hour to write this, and I'm a "casual user" of Python, not a Python expert...

bash$ ./knight2.py 31
+---+---+---+---+---+---+---+---+---+ ... +---+---+---+---+---+---+---+---+---+
|  1|754| 65| 72|  3|756| 77| 80|  5|     |587|478| 13| 90|341|476| 15| 92| 95|
+---+---+---+---+---+---+---+---+---+     +---+---+---+---+---+---+---+---+---+
| 66| 71|  2|755| 76| 73|  4|887|762|     | 12| 89|528|477| 14| 91| 94|335| 16|
+---+---+---+---+---+---+---+---+---+     +---+---+---+---+---+---+---+---+---+
|753| 64|759| 74|757|886|761| 78| 81|     |535|586|479|340|481|342|475| 96| 93|
+---+---+---+---+---+---+---+---+---+     +---+---+---+---+---+---+---+---+---+
...                                                                        ...
+---+---+---+---+---+---+---+---+---+     +---+---+---+---+---+---+---+---+---+
|128|125|414| 49|130|123|410| 47|136|     |206| 39|172|113|162| 37| 34|111| 30|
+---+---+---+---+---+---+---+---+---+     +---+---+---+---+---+---+---+---+---+
|415| 50|129|124|413| 48|131|122|133|     |159|114|161| 38|173|112| 31| 36| 33|
+---+---+---+---+---+---+---+---+---+ ... +---+---+---+---+---+---+---+---+---+

Index

Updated: Sat Oct 8 12:33:59 2022