(July 2011)
 
Posted on Reddit and Hacker News.
 

Implementing a Score4 (Connect Four) engine

The Score 4 (Connect 4) game.

I recently took a one week vacation and went to my parent's village. My niece Theodora was there (she is 7 years old), spending a fortnight with her grandparents. Naturally, in my duties as her uncle, I read her fairy tales when she went to sleep; gave her my phone so she could snap photos and play mobile games; and when she got tired of running around in the garden, we played two-player board and card games.

She particularly enjoyed playing Score4, a tic-tac-toe where you drop chips from the top: the goal is to align a series of 4 of the same color (horizontally, vertically or diagonally) to win. The game is also known as Connect Four in other countries.

Since I always try to find ways to "lure" my nephews and nieces towards science and engineering, I saw an opportunity here: after a number of Score4 rounds (seeing her brain adapt and learn patterns was quite a sight in itself), I told Theodora that by being an engineer, her uncle could create a "magical" program on her laptop: one that would play Score4 so well, that it would beat her, me, and every other human she knows.

She smiled and said "I'd like to see that, uncle!"... and that's when this story started.

Minimax

The Minimax algorithm

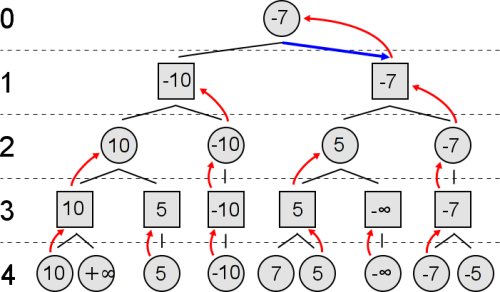
With (1) the scoring function, and (2) a way to "find the allowed moves for a particular board", one can create a tree like the one shown above. Each node represents a board state, with the root node representing the current state of the board. From the root, we recurse downwards, creating the possible boards that can happen by each of the allowed moves, and stop when we reach a specified depth.

When we reach the maximum depth level, we apply the scoring function. This creates scores for all the "leaf" nodes of the tree. We then apply a simple strategy:

• if the level corresponds to a move of the B player, we "distill" the minimum of the children scores to their parent (since the B player wants as negative values as possible)
• if the level corresponds to a move of the A player, we "distill" the maximum of the children scores to their parent (since the A player wants as positive values as possible)

First attempt: Coding Minimax in functional languages (OCaml/F#)

But let's take this one step at a time.

As we saw in the previous section, to implement Minimax we need to be able to represent the board:

type mycell =
    | Orange
    | Yellow
    | Barren

type boardState = mycell array array

The problem has some parameters - the size of the board, the depth we will descend into, as well as the two "magic" return values of the scoring function, which indicate one of the two players has won:

(* size of the board *)
let width = 7
let height = 6

(* depth we will descend *)
let maxDepth = 7

(* scoring function magic constants *)
let orangeWins = 1000000
let yellowWins = -orangeWins

let scoreBoard board =
    ...

let dropDisk board column color =
    ...

let findValidMoves board =
    0--(width-1) |> List.filter (fun column -> board.(0).(column) = Barren)

let performMoves board validMoves color =
    validMoves |> List.map (fun column -> (column,dropDisk board column color))

let rec minimax maximizeOrMinimize color depth board =
    match depth with
    | 0 -> (None,scoreBoard board)
    | _ ->
        let validMoves = findValidMoves board in
        match validMoves with
        | [] -> (None,scoreBoard board)
        | _  ->
            let validMovesAndBoards = performMoves board validMoves color in
            let killerMoves =
                let targetScore = 
		    if maximizeOrMinimize then orangeWins else yellowWins in
                validMovesAndBoards |> 
		List.map (fun (column,board) -> (column,scoreBoard board)) |>
                List.filter (fun (_,score) -> score = targetScore) in
            match killerMoves with
            | (killerMove,killerScore)::rest -> (Some(killerMove), killerScore)
            | [] ->
                let validBoards = validMovesAndBoards |> List.map snd in
                let bestScores = validBoards |>
                    List.map (minimax (not maximizeOrMinimize)
			(otherColor color) (depth-1)) |>
                    List.map snd in
                let allData = myzip validMoves bestScores in
                if !debug && depth = maxDepth then
                    List.iter (fun (column,score) ->
                        Printf.printf "Depth %d, placing on %d, Score:%d\n%!" 
			    depth column score) allData ;
                let cmpScore (_,score1) (_,score2) = compare score1 score2 in
                let (bestMove,bestScore) =
                    match maximizeOrMinimize with
                    | true -> allData |> List.fast_sort cmpScore |> 
                        List.rev |> List.hd
                    | _    -> allData |> List.fast_sort cmpScore |> 
                        List.hd in
                (Some(bestMove),bestScore)

First, we check to see what depth we are in. In this implementation, minimax's depth parameter starts from maxDepth, and is decreased at each recursive call. This means that when the value is 0, we are at the leaf level (see diagram above) - so we invoke the scoreBoard function, passing our input board to it. The function returns an integer value, which we return inside a tuple: (None, score).

Why a tuple, you ask? Simple: minimax will not only find the optimal score - it also needs to find the optimal move, the move that attains that score. The first member of the returned tuple will therefore be the move itself, followed by the score attained by the move.

You might ask: Why do we return None, then, in the place for the move? Well, at depth 0, we don't know what move lead us here (i.e. which column we placed the chip that lead to this board) - it is the parent minimax call that knows. We will see how we handle this below - keep reading.

If we are not at depth 0, we find the validMoves:

let findValidMoves board =
    0--(width-1) |> List.filter (fun column -> board.(0).(column) = Barren)

...
       	let validMoves = findValidMoves board in ...

This means that validMoves is a list of integers: the columns whose top cell is empty.

What were these "--" and "|>"? Well, OCaml allows creation of infix operators (by placing the operator name within parentheses), and I used "--" to emulate the ".." operator that other languages have: The construct N--M generates a list of numbers, starting with number N and ending on number M. In the same vein (i.e. syntactic sugar), "|>" is the "piping" operator:

let (--) i j = (* [X .. Y] construct of F# *)
    let rec aux n acc =
        if n < i then acc else aux (n-1) (n :: acc)
    in aux j []

let ( |> ) x fn = fn x (* piping operator *)

You see now the resemblance with UNIX shell pipes, in the validMoves calculation? We piped a list of 0 .. (width-1) to List.filter, and some of them "survived". Below you'll see lengthier pipes, but the premise is again the same: we pipe stuff from one "function layer" to the next. Infix operators allow us to create "chains" of processing logic, which can be thought of as factory assembly lines.

Once we have the list of valid moves, we check to see if it is empty. If there are no valid moves, we just return the score of our current board, in a (None,score) tuple:

match validMoves with
| [] -> (None,scoreBoard board)
| _  -> ...

If there are valid moves, then we create a list of the valid boards that are instantiated from our valid moves: We pipe the validMoves list to List.map, and for each valid move, List.map creates a tuple. The first element of the tuple is the move itself (the integer pointing to the column). The second element of the tuple is the new board that is created when we drop a chip on that column, via the dropDisk function:

let performMoves board validMoves color =
    validMoves |> List.map (fun column -> (column,dropDisk board column color))

	let validMovesAndBoards = performMoves board validMoves color in ...

We now check if any of these boards are winning/losing boards. Depending on the level we are, we are either maximizing or minimizing the score (i.e. we try to find the optimal move for the Orange OR for the Yellow player), so targetScore is made to point to the "magic" value that, when returned from scoreBoard, declares a victory. We then "filter" for that target score:

let killerMoves =
    let targetScore = if maximizeOrMinimize then orangeWins else yellowWins in
    validMovesAndBoards |> 
        List.map (fun (column,board) -> (column,scoreBoard board)) |>
        List.filter (fun (_,score) -> score = targetScore) in
match killerMoves with
| (killerMove,killerScore)::rest -> (Some(killerMove), killerScore)
| [] -> ...

Did the killerMoves find anything? If yes, then any of them (e.g. the first) are enough to end the game - so pick them out from the head of the list, and return them.

If not, we need to perform recursion, and descend down into derived boards:

let validBoards = validMovesAndBoards |> List.map snd in
let bestScores = validBoards |>
    List.map (minimax (not maximizeOrMinimize) (otherColor color) (depth-1)) |>
    List.map snd in

This is the key line in the function: it recursively descends into depth-1, toggling the color (via function otherColor), toggling the "target mode" from A player to B player and vice versa (i.e. toggling maximizeOrMinimize), and returning a tuple, containing the winning move, and its score. We pipe to List.map snd, and are therefore ignoring the returned moves - we just keep the scores of our "children" nodes in an output list.

Using myzip (which is a function that, just like F#'s List.zip, takes 2 lists as inputs, and creates an output with a single list of 2-tuples), we "pack" all our results in allData: a list of 2-tuples, of the form: (move,score)

Skipping over the debug output, there is only one thing remaining: to sort the results, based on their score, and take the largest or the smallest one, depending on which player we are optimizing for (maximizeOrMinimize).

let cmpScore (_,score1) (_,score2) = compare score1 score2 in
let (bestMove,bestScore) =
    match maximizeOrMinimize with
    | true -> allData |> List.stable_sort cmpScore |> List.rev |> List.hd
    | _    -> allData |> List.stable_sort cmpScore |> List.hd in
(Some(bestMove),bestScore)

Update: Reddit and Hacker News people pointed out that we don't really need to sort - we just need to find the largest/smallest value, so List.fold_left is perfect for the job (and tail-recursive). The benchmarks show no improvement in execution speed for either OCaml or F# with this change, probably because the lists are too short - but regardless, this is indeed the correct way to find the best value:

let best  (_,s as l) (_,s' as r) = if s > s' then l else r
and worst (_,s as l) (_,s' as r) = if s < s' then l else r in
let bestMove,bestScore =
    List.fold_left 
	(if maximizeOrMinimize then best else worst) 
        (List.hd allData) 
        (List.tl allData) in
(Some(bestMove),bestScore)

That's all. Notice that the code reasons about boards, moves, and scores - it is completely generic, and applies to any two-player game that we can code a scoring function for.

Speaking of the scoreBoard function, I tried various forms to evaluate the board. I ended up on a simple policy: measuring how many chips of the same color exist, in spans of 4 going in any direction. I do this over each of the board's cells, and then aggregate this in a table keeping the aggregates from -4 to 4:

• -4 means that the cell is a part of 4 cells that contain 4 yellow chips
• -3 means that the cell is a part of 4 cells that contain 3 yellow chips
• ...
• 3 means that the cell is a part of 4 cells that contain 3 orange chips
• 4 means that the cell is a part of 4 cells that contain 4 orange chips

Let me reiterate again, that all the code above, is NOT problem-specific! If you define your board type, your findValidMoves and your performMoves functions, this code will play whatever game you want. Functional languages offer impressive code abstraction.

Testing with a "driver" program

bash$ engine o53 y52

The engine returns...

3
bash$ ...

...meaning that the engine chose to play on column 3. The Python "driver" program makes use of this simple command line interface, and offers this "graphical" console:

home:/home/ttsiod/score4$ ./interfaces/driver.py 
[                   ]
[                   ]
[                   ]
[                   ]
[                   ]
[         X         ]
--------------------
 0  1  2  3  4  5  6

"q" to quit, or column number (0-6): --> 2
[                   ]                    |
[                   ]                    |
[                   ]         I entered "2" here, so I played my "O" at column 2
[                   ]
[                   ]
[      O  X         ]
--------------------
 0  1  2  3  4  5  6

Computer chose 3 

[                   ]
[                   ]
[                   ]
[                   ]
[         X         ]
[      O  X         ]
--------------------
 0  1  2  3  4  5  6

"q" to quit, or column number (0-6): -->

Well, how deep can we go? Why not go to level 7?

Execution speed

bash$ /c/Program\ Files/Microsoft\ F#/Fsc.exe --checked- --optimize+ score4.fs
bash$ echo "This is F# (functional)"
bash$ time ./score4.exe o53 y43 -debug
Depth 7, placing on column 0, Score:2
Depth 7, placing on column 1, Score:8
Depth 7, placing on column 2, Score:8
Depth 7, placing on column 3, Score:8
Depth 7, placing on column 4, Score:8
Depth 7, placing on column 5, Score:8
Depth 7, placing on column 6, Score:2
5
real    0m8.023s
user    0m7.941s
sys     0m0.013s

bash$ ocamlopt -unsafe -rectypes -inline 1000 -o ./score4.bin score4.ml
bash$ echo "This is OCaml (functional)"
bash$ time ./score4.bin o53 y43 -debug
Depth 7, placing on column 0, Score:2
Depth 7, placing on column 1, Score:8
Depth 7, placing on column 2, Score:8
Depth 7, placing on column 3, Score:8
Depth 7, placing on column 4, Score:8
Depth 7, placing on column 5, Score:8
Depth 7, placing on column 6, Score:2
5

real    0m1.728s
user    0m1.703s
sys     0m0.000s

Native compilers have "unfair" advantages over VMs (in this case, .NET). Then again, F# is a relatively new language; it's compiler will undoubtedly improve over time (Or maybe I am missing some optimization option - any feedback on this most welcome). Let's see what the more mature C# compiler can do on the same platform...

Moving to imperative style (C#/OCaml/F# and eventually, C++)

public static void minimax(
    bool maximizeOrMinimize, Mycell color, int depth, Board board, 
    out int move, out int score)
{
    if (0 == depth) {
	move = -1;
	score = ScoreBoard(board);
    } else {
	int bestScore=maximizeOrMinimize?-10000000:10000000;
	int bestMove=-1;
	for (int column=0; column<width; column++) {
	    if (board._slots[0][column]!=Mycell.Barren)
		continue;
	    int rowFilled = dropDisk(board, column, color); // damage the state
	    if (rowFilled == -1)
		continue;
	    int s = ScoreBoard(board);
	    if (s == (maximizeOrMinimize?orangeWins:yellowWins)) {
		bestMove = column;
		bestScore = s;
		board._slots[rowFilled][column] = Mycell.Barren;
		break;
	    }
	    int moveInner, scoreInner;
	    minimax(
		!maximizeOrMinimize, 
		color==Mycell.Orange?Mycell.Yellow:Mycell.Orange, 
		depth-1, 
		board, 
		out moveInner, out scoreInner);
	    board._slots[rowFilled][column] = Mycell.Barren; // Undo the damage
	    if (depth == maxDepth && g_debug)
		Console.WriteLine(
		    "Depth {0}, placing on {1}, score:{2}", 
		    depth, column, scoreInner);
	    // No need for lists and sorting - just keep the best value you meet.
	    if (maximizeOrMinimize) {
		if (scoreInner>=bestScore) {
		    bestScore = scoreInner;
		    bestMove = column;
		}
	    } else {
		if (scoreInner<=bestScore) {
		    bestScore = scoreInner;
		    bestMove = column;
		}
	    }
	}
	move = bestMove;
	score = bestScore;
    }
}

• We use two "out" parameters to return the results (instead of a tuple).
• We no longer use lists everywhere - we use loops instead.
  (Functional language tutorials tend to favor lists - loops are somewhat "tainted" by imperative thinking. Still, OCaml does offer us for loops - no break, though)
• We mutate the heck out of everything, altering the state wherever we see fit to do so.
• For example, why have dropDisk return a new board? Why not just have it return the row where the chip fell on, modify (in-place) the board, call minimax, and after it returns, "undo" the damage and reset that cell to Barren?
• In the same vein, why store results in lists, and sort them? Why not just keep the best combo (move,score) as we go through the for loop in a couple of mutable variables (references)?

And so we hack and slash - the beautiful abstract functional code is translated to a problem-specific mutant...

Was it worth it?

bash$ csc.exe  /checked- /optimize+ /unsafe+ score4.cs
bash$ echo "This is C# (imperative)"
bash$ time ./score4.exe o53 y43 -debug
Depth 7, placing on column 0, score:2
Depth 7, placing on column 1, score:8
Depth 7, placing on column 2, score:8
Depth 7, placing on column 3, score:8
Depth 7, placing on column 4, score:8
Depth 7, placing on column 5, score:8
Depth 7, placing on column 6, score:2
5

real    0m3.527s
user    0m3.401s
sys     0m0.123s

bash$ /c/Program\ Files/Microsoft\ F#/Fsc.exe --checked- --optimize+ score4_imperative.fs
bash$ echo "This is F# (imperative)"
bash$ time ./score4_imperative.exe o53 y43 -debug
Depth 7, placing on column 0, Score:2
Depth 7, placing on column 1, Score:8
Depth 7, placing on column 2, Score:8
Depth 7, placing on column 3, Score:8
Depth 7, placing on column 4, Score:8
Depth 7, placing on column 5, Score:8
Depth 7, placing on column 6, Score:2
5

real    0m6.161s
user    0m6.143s
sys     0m0.007s

bash$ ocamlopt -unsafe -rectypes -inline 1000 -o ./score4_imperative.bin score4_imperative.ml
bash$ echo "This is OCaml (imperative)"
bash$ time ./score4_imperative.bin o53 y43 -debug
Depth 7, placing on column 0, Score:2
Depth 7, placing on column 1, Score:8
Depth 7, placing on column 2, Score:8
Depth 7, placing on column 3, Score:8
Depth 7, placing on column 4, Score:8
Depth 7, placing on column 5, Score:8
Depth 7, placing on column 6, Score:2
5

real    0m1.424s
user    0m1.400s
sys     0m0.010s

I still feel that bitter taste in my mouth, though - there were speed gains, undoubtedly, but were they worth it?

The high-powered plasma cannon: C++

bash$ g++ -O3 -o score4.bin score4.cpp
bash$ echo "This is C++ (imperative)"
bash$ time ./score4.bin o53 y43 -debug
Depth 7, placing on column 0, score:2
Depth 7, placing on column 1, score:8
Depth 7, placing on column 2, score:8
Depth 7, placing on column 3, score:8
Depth 7, placing on column 4, score:8
Depth 7, placing on column 5, score:8
Depth 7, placing on column 6, score:2
5

real    0m0.226s
user    0m0.220s
sys     0m0.000s

Even when compared to the native binaries generated by functional OCaml, it is running 7.6x times faster.

So... nothing beats C++ speed. Except inline assembly, but let's not get carried away :‑)

Might as well make a GUI, too

The Score 4 GUI - so my niece can play :‑)

You can download a precompiled Win32 binary package of my Score4 implementation from Github (I used py2exe to compile the Python part and MinGW to compile the C++ engine).

Conclusions and lessons learned

bash$ git clone git://github.com/ttsiodras/Score4.git
Cloning into Score4...
remote: Counting objects: 55, done.
remote: Compressing objects: 100% (43/43), done.
remote: Total 55 (delta 16), reused 49 (delta 10)
Unpacking objects: 100% (55/55), done.
bash$ cd Score4
bash$ make benchmark
real    0m0.222s: That was C++
real    0m1.389s: That was OCaml (imperative, C++ mirror)
real    0m1.674s: That was OCaml (functional)
real    0m3.526s: That was C# (imperative, C++ mirror)
real    0m6.184s: That was F# (imperative, C++ mirror)
real    0m7.967s: That was F# (functional)
bash$

• Functional-style programming reasons in terms of higher level constructs: lists of moves, lists of boards, passing around evaluation and move-making functions, etc. Imperative code feels "dirtier", since it reasons in terms of lower-level stuff (for loops on arrays, that usually lead to state mutation...) The results in the functional-style seem more abstract, and easier to reuse. For example, the minimax of the functional implementation can be used as-is for any two-player game.
• There's no such thing as a free lunch, however - imperative code is usually a lot faster. The sweet spot in terms of this balancing act (clear functional code vs speedy execution) - at least in this experiment - was OCaml, a functional language generating native binaries, whose speed resided halfway between VM-based F#/C# and native C++.
• If you do need speed, try utilizing imperative style (state-changing) only in your "core" logic. In this example, scoreBoard (called hundreds of thousands of times) was written imperatively.
• Switching the code to imperative style offers speed advantages, but it causes detrimental effects on quality and reusability. In this particular example, writing minimax imperatively only made sense - i.e. speed gain was significant enough to warrant the code impacts - when C++ was used.
• Separating the presentation logic always helps (easy re-structuring and new features - in this case, a GUI).
• The inclusion of functional constructs (lambdas, etc) and libraries like Boost in C++0x make me eager to see some expert feedback from C++ gurus, who could write the code in a functional manner in C++. Unfortunately, every time I look at Boost my brain bleeds - any help (especially working code) most appreciated.

Enjoy!

Update, July 12: Ports are coming in from all over the Web... the repository now carries versions for:

• Java (Sario O. Alvey)
• Python and D (Reddit/leonardo_m - who also suggested that C++ does not need a 'translation stage' in scoreBoard, since enumerants can be added - hence a 30% speedup in C++)
• Haskell (Hacker News/phnguyen)
• Go (HackerNews/supersillyus)

Update, July 24: Dr Jon Harrop joined in and improved the speed of the F# version of ScoreBoard... by 70%! Just as in my first F# endeavour, his help was invaluable.

Update, July 26: Javascript port, play Score4 in the browser!

Update, July 28: Migrated the F# optimizations (using ints instead of discriminated unions) to other languages, thus avoiding mapping to int values in scoreBoard.

Update, August 7: Added an unordered_map cache to the C++ implementation, to avoid recalculating scores for previously seen boards => 15% speedup.

Update, October 24: Use the best of 10 runs (to minimize impact of OS scheduling artifacts):

Under Linux, using:

    (a) GCC version 4.4.0
    (b) Java 7 
    (c) OCaml 3.12.0
    (d) Mono 2.10.1

...I get:

linux$ make benchmark 
0.067 : C++(imperative,memoized)
0.107 : C++(imperative)
0.124 : C(imperative)
0.378 : Java(imperative)
0.392 : OCaml(imperative)
0.679 : OCaml(functional)
0.835 : F#(imperative)
1.045 : C#(imperative)
2.924 : F#(functional)

Under Windows 7/64bit, and using:

    (a) Cygwin GCC 4.5.0
    (b) Java 7 
    (c) Cygwin OCaml 3.12.0
    (d) C# CSC 3.5.30729.5420, F# FSC 4.0.30319.1

...I get:

win7$ make benchmark 
0.130 : C++(imperative)
0.145 : C++(imperative,memoized)
0.155 : C(imperative)
0.338 : Java(imperative)
0.342 : C#(imperative)
0.395 : F#(imperative)
0.395 : OCaml(imperative)
0.665 : OCaml(functional)
0.947 : F#(functional)

• The Windows .NET compilers and runtimes are running the final, optimized code, a lot faster than Mono does.
• Memoization behaves worse under Cygwin's GCC than the normal algorithm - weird, but consistently reproducible in my machine. In contrast, under Linux it provides a sizeable 40% speed increase.
• The winners are still C++ (for imperative style) and OCaml (for functional style) - but the difference is a lot smaller now between them and the others.

Update, November 6: The recent passing of John McCarthy reminded me of Lisp... so I decided to port score4 to Lisp as well. The tremendous power of Lisp macros allowed me to unroll (at compile-time!) the computations done in scoreBoard and only emit the actual accumulating instructions. This made Lisp the 2nd fastest language, behind only C/C++:

bash$ git clone git://github.com/ttsiodras/Score4.git
...
bash$ cd Score4
bash$ make benchmark
...
======================
= Running benchmarks =
======================
Benchmarking imperative memoized C++ ... 0.089 sec
Benchmarking imperative C++ ... 0.114 sec
Benchmarking imperative C ... 0.119 sec
Benchmarking imperative Lisp (SBCL) ... 0.274 sec
Benchmarking imperative LISP (CMUCL) ... 0.300 sec
Benchmarking imperative OCaml ... 0.304 sec
Benchmarking imperative Java ... 0.376 sec
Benchmarking functional OCaml ... 0.678 sec
...

Here's how the old (commented) and the new code look, for one of the 4 macros:

(defmacro horizontal-spans ()
  ; normal code is...
  ;
  ;(loop for y fixnum from 0 to (1- height) do
  ;  (let ((score (+ (at y 0)  (at y 1) (at y 2))))
  ;    (declare (type fixnum score))
  ;    (loop for x fixnum from 3 to (1- width) do
  ;      (incf score (at y x))
  ;      (myincr)
  ;      (decf score (at y (- x 3))))))
  ;
  ; Loop-unrolling done via this macro:
  ;
  `(progn
    (let ((score 0))
    (declare (type fixnum score))
    ,@(loop for y fixnum from 0 to (1- height)
      collect `(setf score (+ (at ,y 0) (at ,y 1) (at ,y 2)))
      nconc (loop for x fixnum from 3 to (1- width)
        collect `(incf score (at ,y ,x))
        collect `(myincr)
        collect `(decf score (at ,y ,(- x 3)))
        )))))

bash sbcl
...
* (load "score4.cl")
...
* (macroexpand '(horizontal-spans))

(PROGN
 (LET ((SCORE 0))
   (DECLARE (TYPE FIXNUM SCORE))
   (SETF SCORE (+ (AT 0 0) (AT 0 1) (AT 0 2)))
   (INCF SCORE (AT 0 3))
   (MYINCR)
   (DECF SCORE (AT 0 0))
   (INCF SCORE (AT 0 4))
   (MYINCR)
   (DECF SCORE (AT 0 1))
   (INCF SCORE (AT 0 5))
   (MYINCR)
   (DECF SCORE (AT 0 2))
   (INCF SCORE (AT 0 6))
   (MYINCR)
   (DECF SCORE (AT 0 3))
   (SETF SCORE (+ (AT 1 0) (AT 1 1) (AT 1 2)))
   (INCF SCORE (AT 1 3))
   (MYINCR)
   (DECF SCORE (AT 1 0))
   (INCF SCORE (AT 1 4))
   ...

Lisp macros are amazing.